माना किसी चुम्बकीय क्षेत्र B में एक दण्ड चुम्बक ab रखी हुई है , इस चुम्बक के ध्रुव की प्रबलता m है तथा प्रभावी लम्बाई का मान 2L है। इसके अलावा दण्ड चुम्बक तथा चुम्बकीय क्षेत्र के मध्य कोण θ है जैसा चित्र में दिखाया गया है
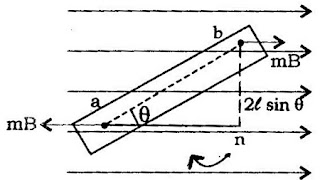
चुम्बकीय क्षेत्र में रखे इस दंड चुम्बक के उत्तरी ध्रुव पर एक बल mB कार्य करेगा जिसकी दिशा चुंबकीय क्षेत्र की दिशा में है।
इसी प्रकार दक्षिणी ध्रुव पर भी इतना ही बल mB कार्य करता है लेकिन इसकी दिशा चुम्बकीय क्षेत्र के विपरीत दिशा में होगी।
ये दोनों बल मिलकर एक बलयुग्म का निर्माण करते है।
इस बल युग्म का बल आघूर्ण (T) = बल x बलों की क्रियारेखा के मध्य लम्बवत दूरी
T = mB x bn
यहाँ bn = 2lsinθ
T = mB 2LBsinθ
चूँकि हम जानते है की चुम्बकीय द्विध्रुव आघूर्ण M = m2L
अतः
T = MBsinθ
कुछ विशेष स्थिति :
1. जब θ = 0 है तो sinθ = 0 अत: T = 0 होगा
इस स्थिति को स्थायी संतुलन की अवस्था कहते है।
2. जब θ = 90 है तो sin90 = 1 अत: T = MB होगा
इस स्थिति में बल आघूर्ण का मान सबसे अधिक होता है।
चुम्बकीय क्षेत्र में चुम्बकीय द्विध्रुव को घुमाने में किया गया कार्य (work done in rotating a magnetic dipole in a magnetic field in hindi):
हमने ऊपर ज्ञात किया है की कोई चुम्बकीय द्विध्रुव आघूर्ण θ कोण पर किसी चुम्बकीय क्षेत्र B में रखा हुआ है तो इस द्विध्रुव पर एक बलयुग्म कार्य करता है जिसका आघूर्ण
T = MBsinθ
माना हमें इस चुम्बक को dθ विक्षेपित करनी है तो इसमें किया गया कार्य
dW = Tdθ
इसी प्रकार θ1 से θ2 स्थिति तक चुम्बकीय द्विध्रुव आघूर्ण को घुमाने में कृत कार्य
Remark:
दोस्तों अगर आपको इस Topic के समझने में कही भी कोई परेशांनी हो रही हो तो आप Comment करके हमे बता सकते है | इस टॉपिक के expert हमारे टीम मेंबर आपको जरूर solution प्रदान करेंगे|